AN142 –侧轴配置中的线性度:需要注意什么?
1. 前言
在侧轴配置中使用 MagAlpha时,需要注意几个准则才能实现传感器的高度线性输出。当磁体旋转时,传感器看到的磁场的两个正交分量具有不同的振幅;通常MagAlpha 角度传感器有一个内置的线性化选项(称为“BCT”)可以对其进行调整。然而事实证明,传感器、磁体位置或磁体磁化方式的某些缺陷都会导致一些误差无法通过 BCT 调整进行补偿。本应用说明将阐述设计人员需要关注的一些特性,以及深入了解各项缺陷后可以实现的线性度,同时还帮助设计人员确定机械和磁体公差。
1.1 理想情况
理想情况下,沿着以磁体为中心的圆形轨迹(见图 1)均匀磁化的有限圆柱体产生的磁场是角度的正弦函数。
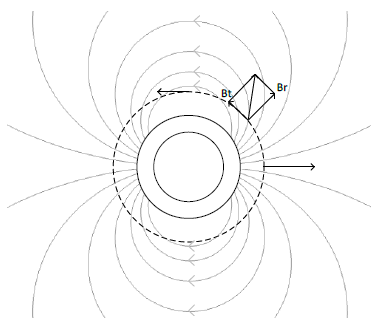
图1 均匀磁化环外的磁力线
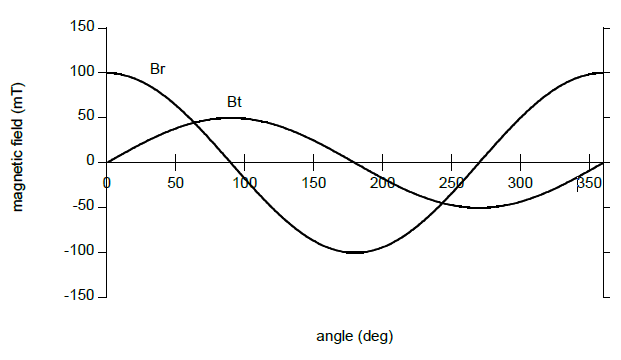
图 2:沿环外圆形轨迹的磁场径向和切向分量
对于有限高度的磁环,一般情况下,Br和Bt的振幅是不同的:$k \equiv Br / Bt \neq 1.$。Br 和 Bt 的解析表达式可参考Caciagli等人所著的 《磁学与磁性材料杂志,456 (2018) 423-432》。幅度不同会导致非线性的传感器输出(即所谓的“椭圆”误差)。该误差曲线本质上具有二次谐波分量,它让一次完整的旋转产生两个正弦波。改变径向和切向灵敏度之间的比率可以很容易地纠正此误差。在 MagAlpha器件中,这个比率由参数“BCT”控制。了解有关 BCT 调整的更多详细信息,请参阅任意一个 MagAlpha 器件数据手册。
侧轴配置是指传感器远离旋转轴的任何配置。图3展示了三种侧轴配置。
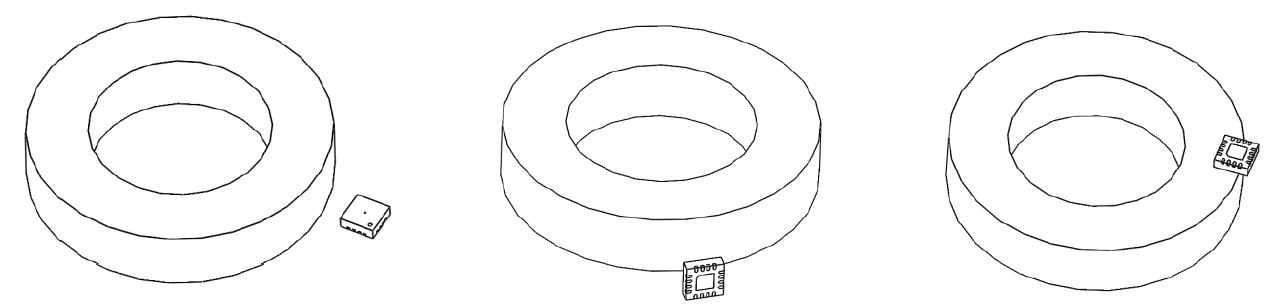
图 3:三种不同的侧轴配置(左:侧环;中:正交;右:顶环)
1.2 实际情况
然而,实际系统中存在的一些缺陷会导致非线性,而且也无法通过任何 BCT 调整得到补偿:
- 位置缺陷:由于系统机械公差导致的磁体和传感器位置不理想
- 磁性缺陷:磁体的磁化不理想
如果产生的误差曲线与二次谐波具有不同的阶次,则 BCT 设置显然无法补偿误差。即使误差是二次谐波,如果相位不同于因k 比率不等于1 所导致的误差曲线,则BCT 设置也无法补偿该误差。即便可以补偿误差,该误差也通常因磁体不同而异,因此需要在生产过程中进行单独校准。
2 位置缺陷
2.1 传感器绕轴旋转
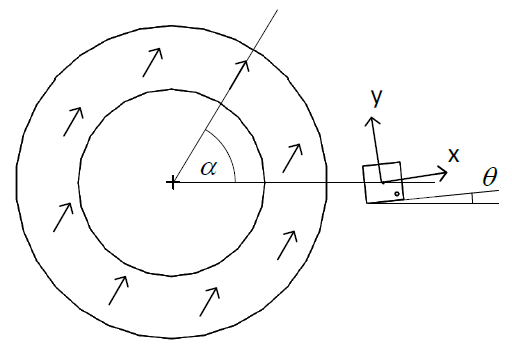
图 4:非理想的传感器方位($\theta$是围绕传感器法线轴的旋转角度)
假设传感器完美对齐,BCT 参数也完美设置以补偿磁场 k 比。如果传感器沿其法线方向旋转,则输出将变得非线性:
$$err = − \frac \theta2 \left(k +\frac1 k + (k − \frac 1 k) cos 2\alpha\right)$$其中$\alpha$为轴角。k 比率越大,误差越大。注意,如果径向分量和切向分量都相等 (k = 1),则输出仅偏移角度$\theta$并保持完美的线性。
和磁场椭圆误差一样,传感器旋转引起的误差主要为二次谐波分量。但相比椭圆误差,这个误差偏移了 45 度。这意味着该误差不能通过 BCT 微调来补偿。这个结果是可以预见的,因为 BCT 参数作用于 x 场与 y 场的灵敏度比率;在传感器旋转的情况下,传感器的 x 分量和 y 分量不能与磁体径向和切向分量对齐。
注意,以上公式适用于任何配置:侧环、正交或顶环。
2.2 磁体偏心
磁体偏心会产生幅度的一次谐波误差(以度为单位),表达为$\frac {2e} r \frac {180} \pi$,其中$e$为偏心度(见图 5)。该表达式在2D环境中是精确的。对有限磁体高度,需另附加一个小的三次谐波分量。
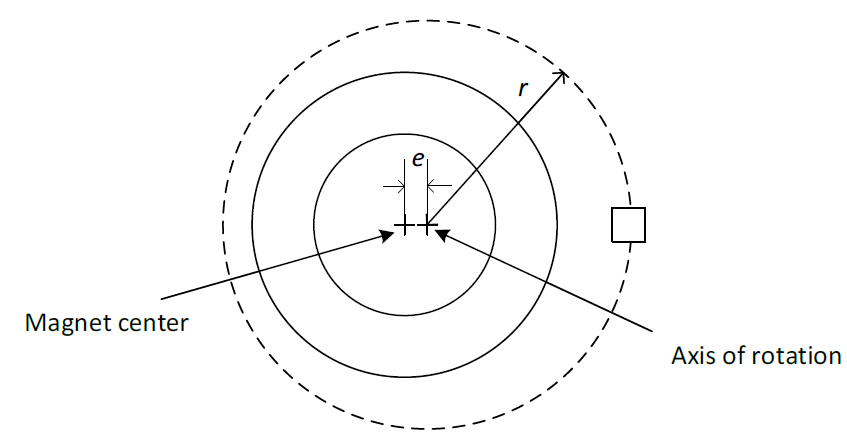
图 5:磁环的偏心(中心偏移距离为$e$)
$\frac {2e} r \frac {180} \pi$幅度适用于侧环配置,也可用于粗略了解正交或顶环配置中的误差。它对顶环配置的影响要大得多,因为偏心会在对磁体旋转一周的k 比率产生很大影响。
2.3 径向或轴向位移
假设针对特定传感器位置完美设置了BCT。此时如果位移因较大 $\Delta k$修改了k比率,则产生的误差为二次谐波曲线:
$$atan ( (1 + \Delta k) tan\ \alpha) \approx \alpha + \frac {\Delta k} 2 sin\ 2\alpha$$这种误差在沿着大梯度$k$值的位移时尤其严重。图 6所示为$k$值的大梯度区域示例。
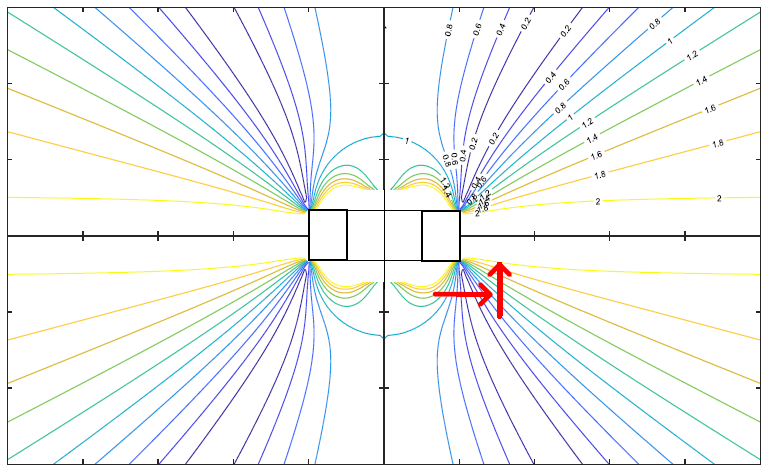
图 6:典型磁环的等$k$值线(大梯度$k$值如红色箭头所示)
由此可知,临界传感器位移为:
- 顶环径向位移
- 正交轴向位移
侧环配置受影响较小(见图 7)。
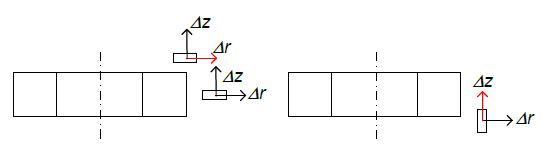
图 7:轴向和径向位移(红色为临界位移)
3. 磁体缺陷导致的误差
制造过程,特别是磁化步骤中,很容易存在缺陷。
3.1 去磁场导致的不均匀性
这种失真常见于所有磁环,尤其是窄壁(即磁环内径接近输出直径)磁环。从性质上来看,其磁化矢量不是平行的,而是倾向于跟随环的曲率(见图 8)。
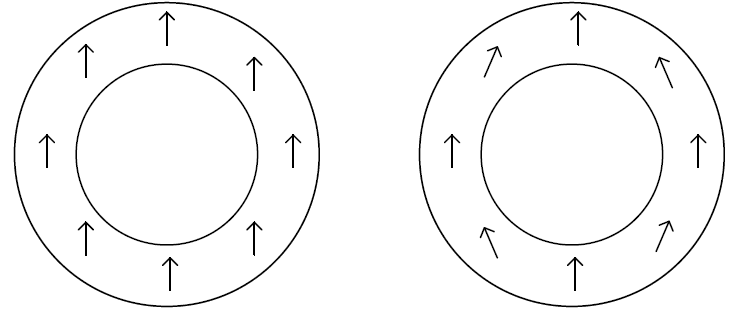
图 8:理想的均匀磁化(左)和实际磁体中的典型磁化(右)
为了使磁环最终被磁化,必须将磁环浸入沿其直径方向的均匀强磁场中。在这一步骤中,局部材料颗粒感受到的总磁场非常关键。该磁场通常称为 H,它是外加磁场(圆柱的远磁场)和“去磁场”(即由圆柱本身相邻颗粒产生的磁场)之和。事实证明,对于一个封闭且较高的圆柱体而言,H 是内部均匀的。因此,所有的磁畴都沿同一方向定向。均匀的圆柱体沿着外部圆形轨迹产生完美的正弦径向、切向和轴向场。磁环(空心圆柱体)的行为则不同,其H 场会出现偏离,如图 9所示。这并不是磁体的默认特性,而是其形状使然。
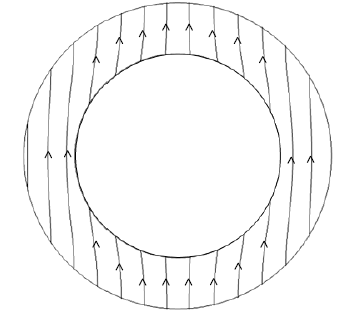
图 9:环内总场 H(由均匀场$H_{ext}$导致)
通常,这种效应使径向(或轴向)场更呈三角形,而切向场更呈“方形”。请参考图 10中的典型失真。
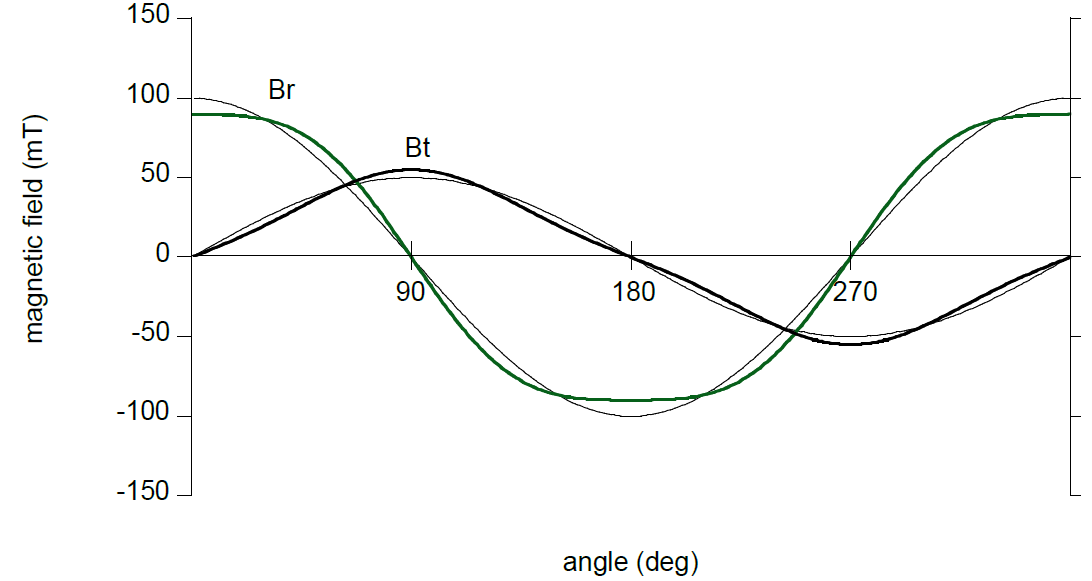
图 10:径向和切向场分量的三次谐波失真
三次谐波失真形式:
$$B_r(\alpha) = B_r^0(cos\ \alpha - D\ cos\ 3\alpha)$$ $$B_t(\alpha) = B_t^0(sin\ \alpha - D\ sin\ 3\alpha)$$其中$D$为失真率(假设两个组件的失真率相同)。当$D$较小时,会导致误差:
$$err = (-D + D^2) sin\ 2\alpha - \frac {D^2} 2 sin\ 4\alpha + ..$$它本质上意味着一个幅度为 $D + D^2 -$ 的二次谐波和幅度为$\frac {D^2} 2$的四次谐波的误差。原则上,二次谐波误差与椭圆误差具有相同的相位,因此可以通过BCT微调来补偿。
3.2 外加磁场不完善导致的不均匀性
磁化器件(或压制过程中的各向异性磁体)内的工件定位不准确可能导致不同的误差。因为其尺寸有限,H 场线并非完全平行。如果工件偏离中心,则磁力线的曲率不对称,将导致一次谐波误差。这会影响所有侧轴配置中的传感器读数。
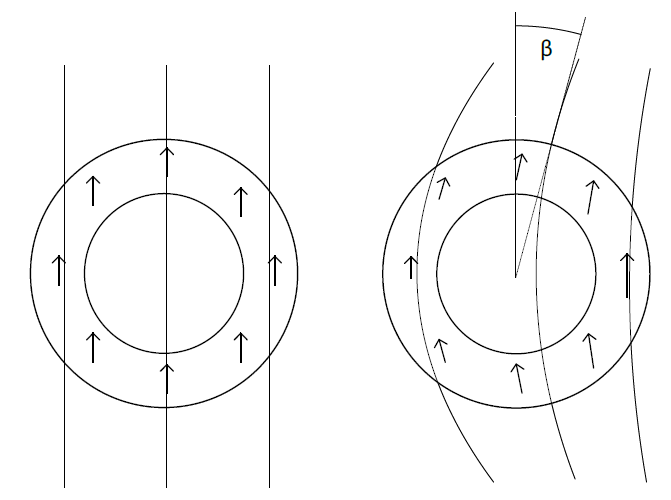
图 11 :理想磁化(左)和磁化器件的不完美定心导致的不均匀性(右);$\beta$ 为纯径向磁场角偏移
测量这种不对称性的方法之一是记录径向或切向场,并寻找一个半圈和另一个半圈之间的不对称性(见图 12)。其产生的传感器误差是振幅为$\beta$的一次谐波误差。
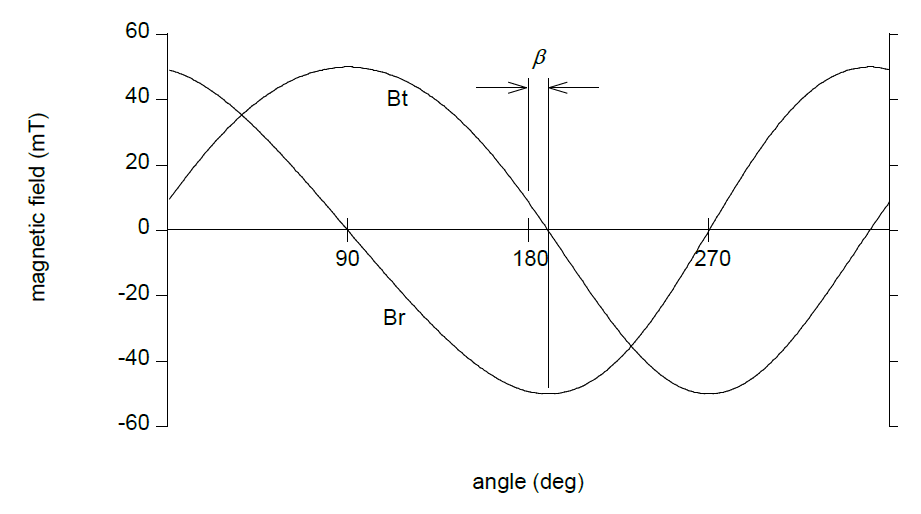
图 12:在未完全磁化的环周围测得的径向和切向场
3.3 磁化倾斜
商用磁环或圆柱的磁化通常都不是严格的平面磁化(即垂直于旋转轴)。相反,磁化矢量可以在轴向方向上倾斜几度($\pm 5$度为常见公差),请参见图 13。
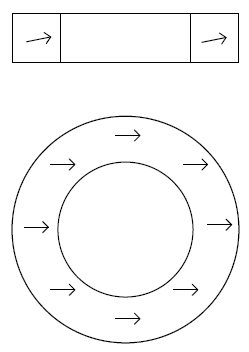
图13: 磁化倾斜
磁化可以看作是理想磁场与纯轴向扰动场的叠加(见图 14)。在侧环配置中,“轴向磁体”产生的磁场垂直于芯片平面,既无法测量(见图 14)。因此,磁化倾斜不会影响侧环传感器的读数;但对于正交或顶环配置则不同。
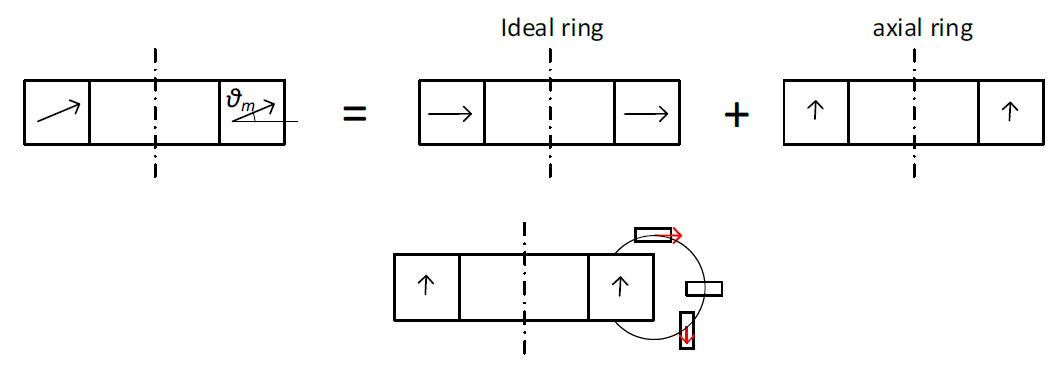
图 14:倾斜可分解为理想的径向磁化和轴向扰动(上)。轴向扰动影响正交和顶环配置(下)
我们可以粗略估算倾斜对正交配置的影响。无论轴角度如何,轴向环都会在传感器位置产生恒定的磁场。当理想磁体的磁场在传感器位置完全切向磁场时,会出现最严重的误差,即寄生磁场垂直于理想磁场:
$$error = atan \left(\frac {B_{axial}}{B_t}\right)$$在传感器接近磁体中间高度且磁体高度较小的情况下,此误差可近似为:
$$error = atan \left(\frac1 2 tan\ \theta_m \right)$$其中$\theta_m$为磁化倾角。
从图 14 中可以观察到,较大误差将影响顶环配置。
4. 总结
| 原因 | 相关参数 | H1 | H2 | H4 | 作用于 | BCT 可否补偿? | ||
| 侧环 | 顶环 | 邻环 | ||||||
| 传感器旋转 | $k$:椭圆率;$\theta$:传感器旋转角度 | 0 | $$atan \left(\frac 1 2 tan\ \theta_m \right)$$ | 0 | 是 | 是 | 是 | 否 |
| 磁体偏心 | $\frac e r$:偏心率与传感器半径之比 | $$\frac {2e} r$$ | 0 | 是 | 是 | 是 | 否 | |
| 传感器径向或轴向位移 | $\Delta k$:椭圆率变化 | 0 | $$\frac {\Delta k}2$$ | 0 | 是 | 是 | 是 | |
| 去磁失真 | $D:3^{rd}$ 谐波失真率 | 0 | $$D - D^2$$ | $$\frac {D^2} 2$$ | 是 | 是 | 是 |
H2 是 - H4 否 |
| 非均匀磁场 | Br 最大值的 $\beta$ 偏移 | $$\beta$$ | 0 | 0 | 是 | 是 | 是 | 否 |
| 磁化倾斜 | $\theta m$:倾角 | $$atan \left(\frac 1 2 tan\ \theta_m \right)$$ | 0 | 0 | 是 | 是 | 否 | |
注:乘以 $\frac {180}\pi$ 即可获得以度为单位的振幅。




直接登录
创建新帐号