Rectifiers, also known as AC/DC converters, are essential components of modern power electronic systems because they convert alternating current (AC) to direct current (DC). Several performance factors decide if these converters are suitable for a certain application. To analyze the performance of AC/DC converters, various key performance characteristics must be considered, including input current harmonic distortion, output ripple voltage, rectifier efficiency, and power factor. Electrical engineers who design and evaluate AC/DC converters for different applications must have an extensive understanding of these characteristics.

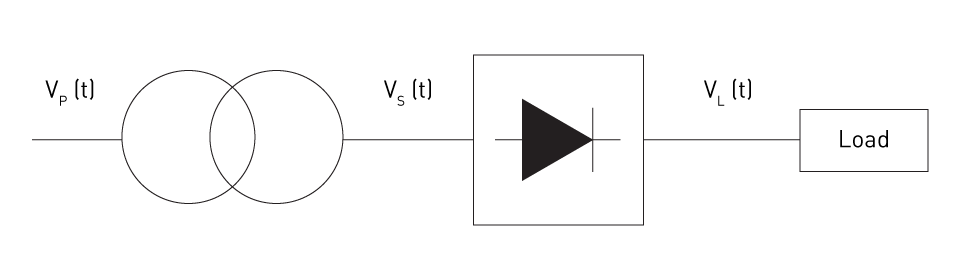
Figure 1: Generic scheme of a rectifier

The figure above depicts the generic scheme of a rectifier, which includes:

• v_p (t) – transformer time-dependent primary voltage
• v_s (t) – transformer time-dependent secondary voltage
• v_L (t) – a time-dependent voltage at the output of the rectifier (on the load)

The DC voltage on the load is the average of the rectifier's output voltage over the period T.

$$V_{DC} = \frac{1}{T} \int_0^T v_L(t) \, dt$$

RMS Voltage

The RMS voltage at the load can be calculated with the following equation:

$$V_L = \sqrt{\frac{1}{T} \int_0^T v_L^2(t) \, dt}$$

Form Factor

The Form Factor (FF) is the ratio of the following two voltages:

$$FF = \frac{V_L}{V_{DC}}$$

Let us suppose that the load itself is a perfect resistance. If this is the case, we can calculate the following currents:

$$i_L(t) = \frac{v_L(t)}{R_L}$$ $$I_{DC} = \frac{V_{DC}}{R_L}$$ $$I_L = \frac{V_L}{R_L}$$

Rectification Efficiency

The rectification ratio (η) or rectification efficiency is represented as:

$$\eta = \frac{P_{DC}}{P_L + P_D}$$

where:

$$P_{DC} = V_{DC} \cdot I_{DC}$$ $$P_L = V_L \cdot I_L$$ $$P_D = R_D \cdot I_L^2$$

In the last equation, P_D represents the rectifier losses, whereas R_D is the rectifier's equivalent resistance. From the previous equations, we obtain:

$$\eta = \frac{V_{DC} \cdot I_{DC}}{V_L \cdot I_L + R_D \cdot I_L^2} = \frac{V_{DC}^2}{V_L^2} \cdot \frac{1}{1 + \frac{R_D}{R_L}}$$

If the switches are perfect (with no losses, RD = 0), the rectification efficiency equals:

$$\eta = \frac{V_{DC}^2}{V_L^2} = \frac{1}{FF^2}$$

Ripple Factor

The Ripple Factor (RF) show the smoothness of the rectifier's output voltage waveform. The RF is defined as the ratio of the effective AC component of the load voltage to the DC voltage.

$$R_F = \frac{\sqrt{V_L^2 - V_{DC}^2}}{V_{DC}} = \sqrt{FF^2 - 1}$$

Transformer Utilization Factor

The Transformer Utilization Factor (TUF) is one of the parameters used to determine the transformer's characteristics.

$$TUF = \frac{P_{DC}}{S_T}$$

where S_T indicates transformer rated (apparent) power.




Displacement Power Factor

The Displacement Power Factor is defined as follows:

$$DPF = \cos(\Phi_1)$$

Φ₁ represents the input displacement angle, which is the angle between the main parts of the AC line current and the line-to-neutral voltage.