四步完成反激式变换器反馈环路补偿器设计

每月为您发送最具参考价值的行业文章
我们会保障您的隐私
简介
反激式变换器因其功能多样、易于设计且成本低廉已成为电力电子领域最为广泛使用的拓扑结构之一。其结构源自三种基本拓扑之一,即升降压拓扑结构。然而,与升降压变换器不同,反激式拓扑还支持输出电压与输入电源之间的电气隔离。该特性对工业和消费电子应用极为重要。
在用于稳定电源变换器的各种控制方法当中,最流行的控制方法称为峰值电流模式控制。该方法通过持续感测原边电流来为电源提供重要的保护功能。此外,为了获得更高设计性能,交叉调节技术也常被用来调节具有重载输出的变换器。
本文的目的是向读者、工程师和学生展示如何正确设计用于稳定反激式变换器的控制环路,从而提供最佳功能。设计流程包括最小化稳态误差、按需增加/减少带宽,以及尽可能提高相位/增益裕度。
闭环反激式变换器功能框图
在针对峰值电流控制模式反激变换器进行稳定控制器所需的计算之前,需要首先理解整个闭环系统的组成部分:变换器平均模型与控制环路(见图1)
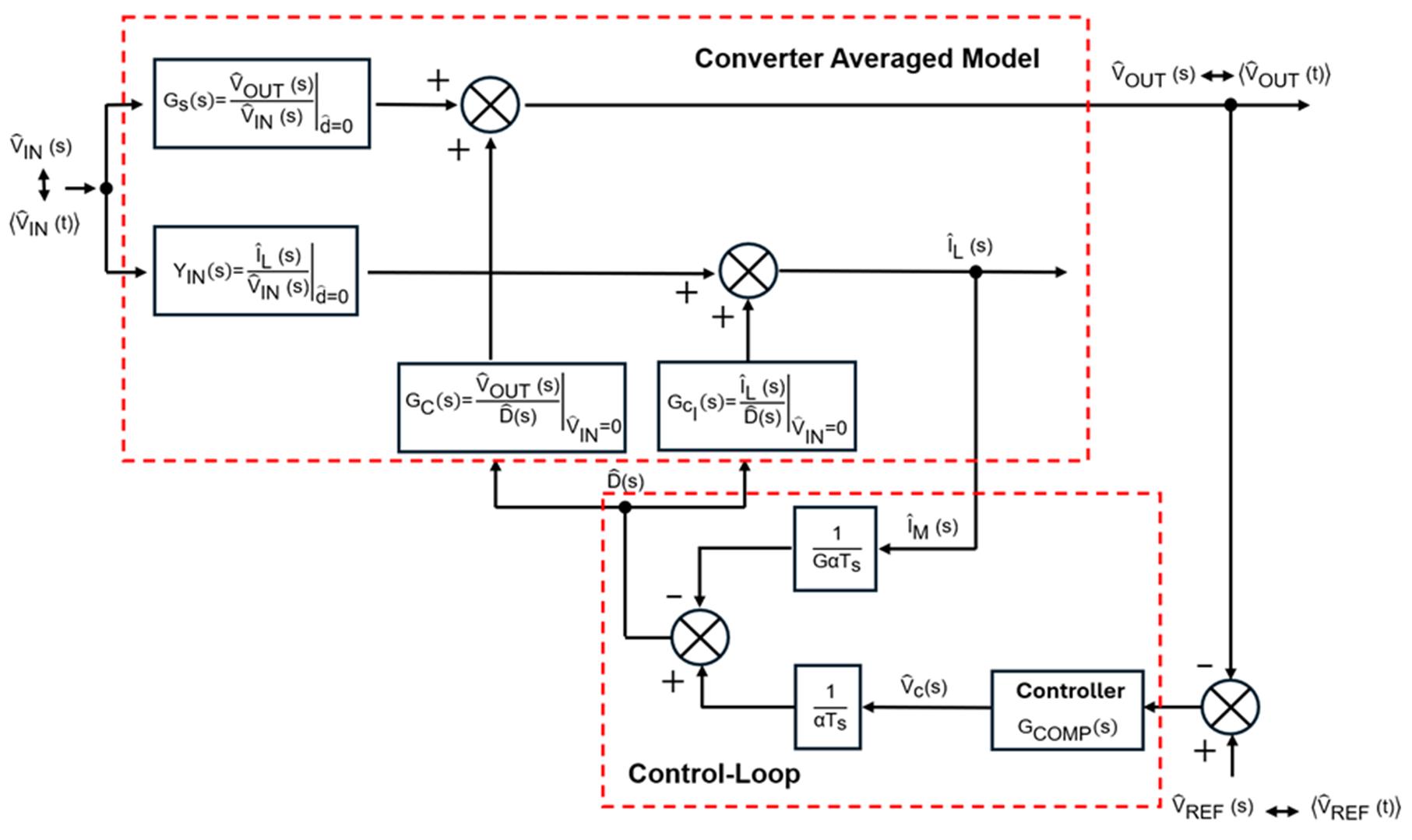
图1:闭环系统功能框图
设计工程师通常对变换器在负载变化下的行为最为关注。假设输入电压(VIN)恒定,通过对占空比小信号扰动下的开环传递函数进行建模,可以研究电源的动态响应特性。
对开环系统可以通过公式(1)来建模:
$$ T_{V0}(s) = \left. \frac{\hat{V}_{OUT}(s)}{\hat{V}_{C}(s)} \right|_{\hat{V}_{IN} = 0} = \frac{G \cdot G_{C}(s)}{G_{CI}(s) + G\alpha T_{s}} $$其中,G 是转换为电压的电流采样增益,GC (s)和GCI (s) 分别为反激式变换器在占空比发生小扰动时输出电压和磁化电流响应的传递函数,GαTS为斜坡补偿模型,用于避免在开关频率的一半处出现双极振荡。
反激式变换器控制设计和元件选择
设计反激式变换器的控制环路涉及很多权衡和考量。后续章节将逐步讲解设计流程。
图2展示了整个设计流程。
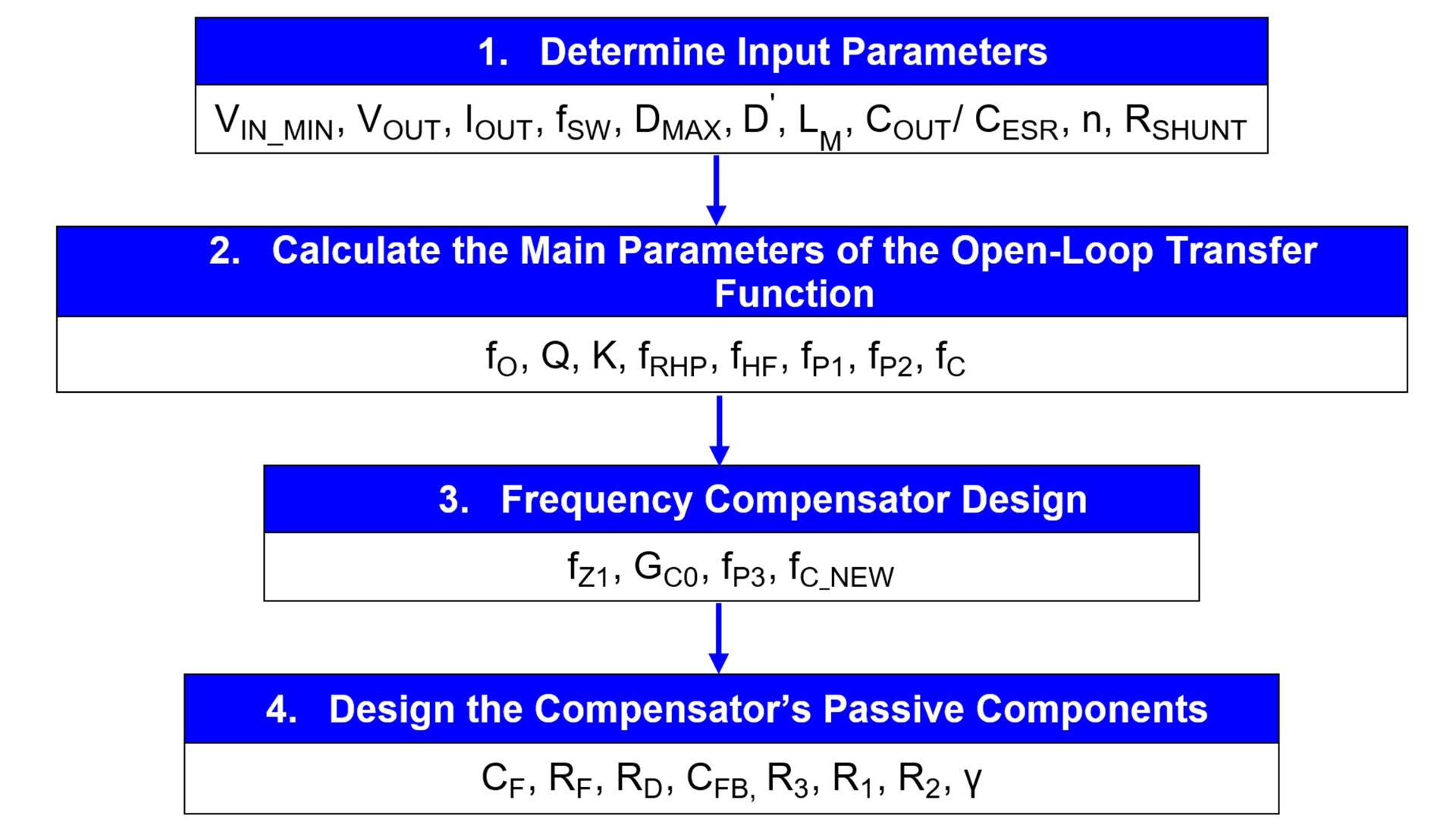
图2:控制环路的设计流程
控制环路设计流程与相关计算
步骤 1:设计输入
首先,根据相关规格确定变换器的主要参数,然后将这些参数定义为控制环路的设计输入。具体参数包括:输入和输出电压(VIN和VOUT)、工作模式、开关频率 (fSW)、占空比、磁化电感 (LM)、匝数比 (NP:NS)、分流电阻 (RSHUNT) 和输出电容 (COUT)。表1列出了本文涉及电路的设计输入。
表 1:设计输入一览
| 设计输入 | 值 |
| 最小输入电压 (VIN_MIN) | 85VAC |
| 输出电压 (VOUT) | 12V |
| 输出电流 (IOUT) | 3.33A |
| 操作模式 | CCM at VIN_MIN |
| 开关频率 (fSW) | 65kHz |
| 最大占空比 (DMAX) | 46% |
| 副边占空比 (D’) | 54% |
| 磁化电感 (LM) | 610µH |
| 输出电容/ESR (COUT/CESR) | 950µF/15mΩ |
| 匝数比 NS:NP (n) | 1/6 |
| 分流电阻 (RSHUNT) | 0.4Ω |
设计反激式变换器补偿器,需要先确定构成变换器的所有主要元件。本文采用MPS HF500 -40反激式稳压器来演示如何利用光耦反馈轻松设计补偿器。HF500-40是一款具有固定频率的电流模式稳压器,内置斜率补偿功能。由于变换器在低线电压输入下工作于连续导通模式 (CCM),因此会在开关频率的一半处产生双极振荡;内置斜率补偿可抑制该振荡,让其影响几乎可以忽略。
第二步:计算开环传递函数的参数
精确计算开环传递函数的参数,并计算补偿器所有参数值,以实现变换器在动态行为层面的优化。
峰值电流控制反激式变换器的开环传递函数(包括补偿斜坡因子)可通过公式(2)估算:
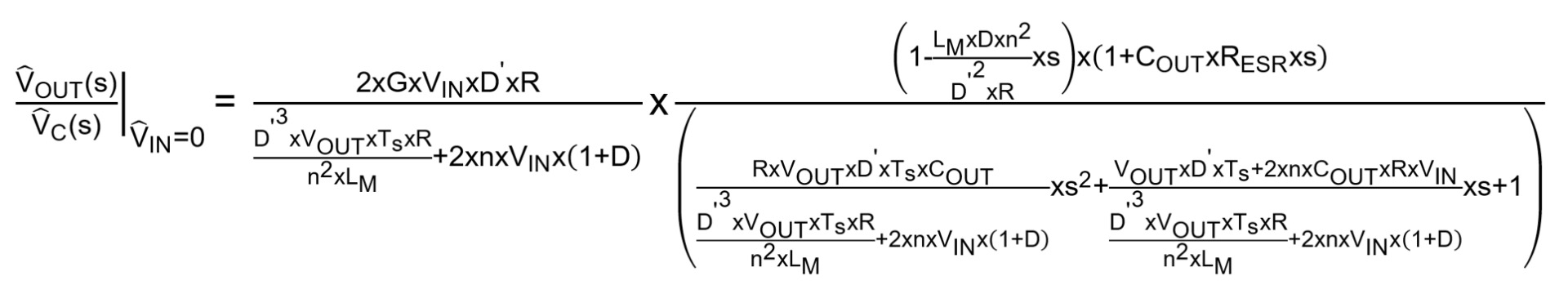
其中 D' 定义为副边二极管(或同步 FET)在开关周期内处于活动状态的时间百分比。
基本规范模型定义如公式(3)所示:
$$ \left. \frac{\hat{V}_{OUT}(s)}{\hat{V}_{C}(s)} \right|_{\hat{V}_{IN} = 0} = G_{C0} \cdot \left(1 - \frac{s}{\omega_{\text{RHP}}} \right) \left(1 + \frac{s}{\omega_{\text{HF}}} \right) \Bigg/ \left[ \left( \frac{s}{\omega_o} \right)^2 + \frac{s}{\omega_o Q} + 1 \right] $$
注意,作为电路中最显著的寄生效应,等效串联电阻( ESR )对输出电容的影响已包含在传递函数中。
利用公式(2)和公式(3),可以计算出关键参数。
谐振频率(fO) 可通过公式(4)计算:
$$ f_O = \frac{\omega_0}{2\pi} = \frac{1}{2\pi} \cdot \sqrt{ \frac{ \left( \frac{{D'}^3 \cdot V_{OUT} \cdot T_s \cdot R}{n^2 \cdot L_M} + 2 \cdot n \cdot V_{IN} \cdot (1 + D) \right) }{ R \cdot V_{OUT} \cdot D' \cdot T_s \cdot C_{OUT} } } $$
输入相关值后,通过公式(5)计算出 fO:
$$ f_0 = \frac{1}{2\pi} \sqrt{ \frac{ \left( \frac{0.54^3 \times 12 \times \frac{12}{3.33}}{ \left( \frac{1}{6} \right)^2 \times 610 \times 10^{-6} \times 65 \times 10^3 } + 2 \times \frac{1}{6} \times 85 \sqrt{2} \times (1 + 0.46) \right) }{ \frac{12}{3.33} \times 12 \times 0.54 \times \frac{1}{65 \times 10^3} \times 950 \times 10^{-6} } } = 2.191 \, \text{kHz} $$
右半平面零点 (fRHP) 可用公式(6)来估算:
$$ f_{\text{RHP}} = \frac{{D'}^2 \cdot R}{2\pi n^2 L_M D} = \frac{0.54^2 \cdot \frac{12}{3.33}}{2\pi \cdot \left( \frac{1}{6} \right)^2 \cdot 610 \times 10^{-6} \cdot 0.46} = 21.46 \, \text{kHz} $$q 因子 (Q) 通过公式 (7) 来计算:
$$ Q = \frac{ \sqrt{ \left( \frac{{D'}^3 V_{OUT} T_s R}{n^2 L_M} + 2 n V_{IN} (1 + D) \right) } \cdot \sqrt{ R V_{OUT} D' T_s C_{OUT} } }{ V_{OUT} D' T_s + 2 n C_{OUT} R V_{IN} } $$
输入相关值后,通过公式(8)估算出Q:
$$ Q = \frac{ \sqrt{ \left( \frac{0.54^3 \cdot 12 \cdot \frac{12}{3.33}}{ \left( \frac{1}{6} \right)^2 \cdot 610 \cdot 10^{-6} \cdot 65 \cdot 10^3 } + 2 \cdot \frac{1}{6} \cdot 85 \sqrt{2} \cdot (1 + 0.46) \right) } \cdot \sqrt{ \frac{12}{3.33} \cdot 12 \cdot 0.54 \cdot \frac{1}{65 \cdot 10^3} \cdot 950 \cdot 10^{-6} } }{ 12 \cdot 0.54 \cdot \frac{1}{65 \cdot 10^3} + 2 \cdot \frac{1}{6} \cdot 950 \cdot 10^{-6} \cdot \frac{12}{3.33} \cdot 85 \sqrt{2} } = 0.034 $$
用公式(9)来计算直流增益(K):
$$ K = \frac{ 2 \cdot G \cdot V_{\text{IN}} \cdot D' \cdot R }{ \frac{{D'}^3 \cdot V_{\text{OUT}} \cdot T_s \cdot R}{n^2 \cdot L_M} + 2 \cdot n \cdot V_{\text{IN}} \cdot (1 + D) } $$ $$ G = \frac{1}{R_{\text{SHUNT}}} $$输入相关值后,通过公式(10)估算出K:
$$ K = \frac{ 2 \cdot \frac{1}{0.4} \cdot 85 \sqrt{2} \cdot 0.54 \cdot \frac{12}{3.33} }{ \frac{ 0.54^3 \cdot 12 \cdot \frac{12}{3.33} }{ \left( \frac{1}{6} \right)^2 \cdot 610 \times 10^{-6} \cdot 65 \times 10^3 } + 2 \cdot \frac{1}{6} \cdot 85 \sqrt{2} \cdot (1 + 0.46) } = 18.08 = 25.14\,\text{dB} $$高频零点 (fHF) 采用公式(11)计算:
$$ f_{\text{HF}} = \frac{1}{2\pi C_{OUT} R_{ESR}} = \frac{1}{2\pi \cdot 950 \times 10^{-6} \cdot 15 \times 10^{-3}} = 16.75\,\text{kHz} $$需要特别指出的是,在电流模式控制下,Q的取值通常远低于0.5。基于这一点,传递函数分母中的二阶多项式最终将分解为两个实部为负的实数极点。这与电压控制模式(或补偿斜坡幅度很大)不同,后者会产生两个共轭复数极点。
两个负实数极点可以通过公式(12)估算:
$$ f_{P1} = Q \cdot f_O = 0.034 \times 2191 = 74.5\,\text{Hz} \quad \text{and} \quad f_{P2} = \frac{f_O}{Q} = \frac{2191}{0.034} = 64.44\,\text{kHz} $$新的开环传递函数可用公式(13)计算:
$$ \left. \frac{\hat{V}_O(s)}{\hat{V}_C(s)} \right|_{\hat{V}_g = 0} = K \cdot \frac{ \left(1 - \frac{s}{\omega_{\text{RHP}}} \right) \left(1 + \frac{s}{\omega_{\text{HF}}} \right) }{ \left(1 + \frac{s}{\omega_{p1}} \right) \left(1 + \frac{s}{\omega_{p2}} \right) } = 25.14 \cdot \frac{ \left(1 - \frac{s}{2\pi \cdot 21.46 \cdot 10^3} \right) \left(1 + \frac{s}{2\pi \cdot 16.75 \cdot 10^3} \right) }{ \left(1 + \frac{s}{2\pi \cdot 74.5} \right) \left(1 + \frac{s}{2\pi \cdot 64.44 \cdot 10^3} \right) } $$截止频率 (fC)通过公式(14)估算: $$ f_C = f_{P1} \cdot K = 74.5 \times 18.08 = 1.35\,\text{kHz} $$
下文将解释频率补偿器设计如何实现电源稳定性和优异的性能。
步骤3:频率补偿器设计
一旦完成开环传递函数建模,就需要设计频率补偿器来实现最佳性能。由于上述传递函数的频率响应有两个独立极点(一个在低频,一个在高频),因此可设计一个简单的II型补偿器,该补偿器不需要额外零点。电压控制模式则需要引入零点补偿,因其存在导致谐振的双极点。
为了最大限度地减小稳态误差,需设计一个反向零点(或在原点设置极点),以便在低频段提供更高增益。为确保系统稳定性不受影响,其频率应比首个极点至少低 10 倍,计算公式 (15)如下:
$$ f_{Z1} \leq \frac{f_{P1}}{10} \;\Rightarrow\; f_{Z1} \leq \frac{74.5}{10} \;\Rightarrow\; f_{Z1} \leq 7.45\,\text{Hz} $$由于高频段存在ESR寄生效应,因此还需设计一个高频极点来补偿并去除该效应。该极点估算公式(16)如下:
$$ f_{P3} \approx f_{HF} \;\Rightarrow\; f_{P3} \approx 16.75\,\text{kHz} $$除此之外,通过修改截止频率来实现更高/更低带宽,提供更快/更慢动态响应也是一种常见手段。一旦选定截止频率(在本例中, fC 增加到6.5kHz ,或fSW的10% ),就可以用公式 (17) 来计算补偿器的中频增益:
$$ G_{\text{COMP}} = \frac{f_{C,\text{NEW}}}{f_{P1}} \cdot \frac{1}{K} \cdot \frac{ \sqrt{1 + \left( \frac{\omega_{z1}}{\omega_{C,\text{NEW}}} \right)^2} }{ \sqrt{1 + \left( \frac{\omega_{C,\text{NEW}}}{\omega_{P3}} \right)^2} } = \frac{6.5 \times 10^3}{74.5} \cdot \frac{1}{18.08} \cdot \frac{ \sqrt{1 + \left( \frac{2\pi \cdot 7.45}{2\pi \cdot 6.5 \times 10^3} \right)^2} }{ \sqrt{1 + \left( \frac{2\pi \cdot 6.5 \times 10^3}{2\pi \cdot 16.75 \times 10^3} \right)^2} } = 4.5 = 13.06\,\text{dB} $$完成补偿器频率范围设计之后,需要计算无源元件的取值。
步骤4:设计补偿器的无源元件
为了稳定带交叉调节的电流控制模式反激式变换器,最常用的II 型补偿器均采用光耦反馈(见图 3)。
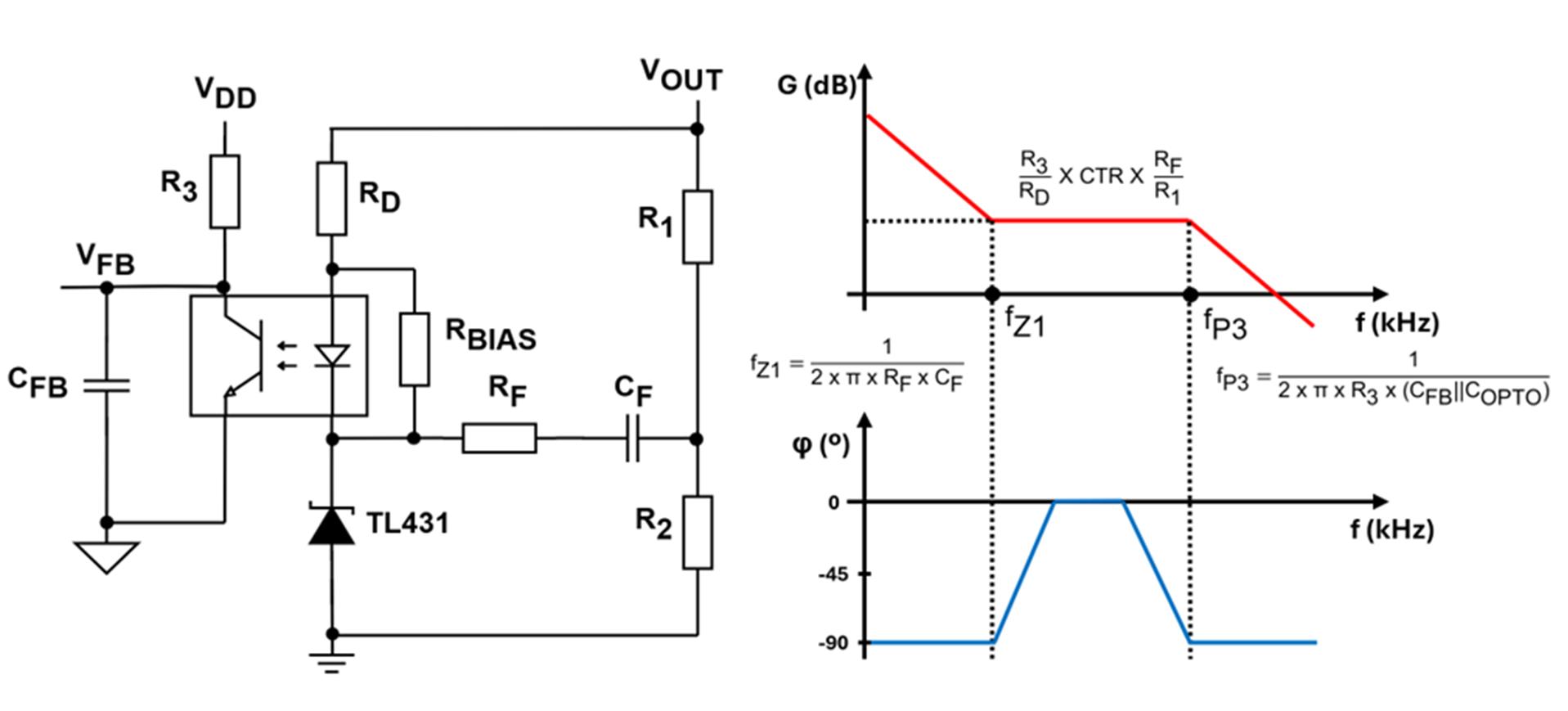
图3:采用光耦反馈的II型补偿器
采用光耦反馈的补偿器传递函数可用公式(18)估算:
$$ G_{\text{COMP}}(s) = - \frac{R_3}{R_D} \cdot \text{CTR} \cdot \frac{R_F}{R_1} \cdot \frac{1 + R_F C_F s}{s \left[ R_3 \left( C_{\text{FB}} \parallel C_{\text{OPTO}} \right) s + 1 \right]} $$中频增益由两级构成:光耦增益和可调电压基准补偿器增益,计算公式(19)如下:
$$ \left\| G_{\text{COMP}} \right\| = \frac{R_3}{R_D} \cdot \text{CTR} \cdot \frac{R_F}{R_1} $$计算出最大电阻对正确偏置光耦也非常重要。通过公式(20)可估算该电阻值:
$$ R_D \leq \frac{ \left( V_{OUT} - V_F - V_{\text{DZ1,MIN}} \right) \cdot R_3 \cdot \text{CTR}_{\text{MIN}} }{ V_{DD} - V_{\text{CE,SAT}} + \text{CTR}_{\text{MIN}} \cdot R_3 \cdot I_{\text{BIAS}} } $$计算RD 所需的参数可在光耦和可调电压基准数据手册中查得。表2列出了这些光耦参数的典型值。
表2:主要光耦参数
| 输入参数 | 值 |
| 正向电压 (VF) | 1V |
| 偏置电流 (IBIAS) | 1mA |
| 光耦最小电流传输比 (CTRMIN) | 0.3 |
| 光耦标称电流传输比 (CTR) | 1 |
| 集电极-发射极饱和电压 (VCE_SAT) | 0.2V |
| 光耦输出电容 (COPTO) | 200pF |
表 3 列出了可调电压基准参数的典型值。
表3:可调电压基准参数
| 输入参数 | 值 |
| 最小基准电压 (VDZ1_MIN) | 2.495V |
| 反馈电阻 (R1) | 100kΩ |
| 反馈电阻 (R2) | 26.3kΩ |
| 最大 VFB | 3.9V |
获得上述参数之后,即可通过公式(21)计算 RD:
$$ R_D \leq \frac{ \left( V_{OUT} - V_F - V_{\text{DZ1,MIN}} \right) \cdot R_3 \cdot \text{CTR}_{\text{MIN}} }{ V_{DD} - V_{\text{CE,SAT}} + \text{CTR}_{\text{MIN}} \cdot R_3 \cdot I_{\text{BIAS}} } \leq \frac{ (12 - 1 - 2.495) \cdot 12 \times 10^3 \cdot 0.3 }{ 3.9 - 0.2 + 0.3 \cdot 12 \times 10^3 \cdot 1 \times 10^{-3} } \leq 4.2\,\text{k}\Omega $$获取 R3 值(在本例中,R3 位于HF500 -40 控制器内部,最小值12kΩ),以及 R1, R2, 和RD ( RD = 2kΩ)之后,再通过公式 (22) 估算 RF :
$$ R_F = \frac{G_{\text{COMP}}}{\dfrac{R_3}{R_D} \cdot \text{CTR}_{\text{NOM}}} \cdot R_1 = \frac{4.5}{\left( \dfrac{12 \times 10^3}{2 \times 10^3} \cdot 1 \right)} \cdot 100 \times 10^3 = 75\,\text{k}\Omega $$其中, GCOMP 为补偿器中频增益,通过公式(17)计算得出。该参数用于调整电源带宽。
基于之前得出的反向零点和高频极点,分别用公式(23)和公式(24)计算 CF and CFB:
(23)
$$ f_{z1} = \frac{1}{2\pi R_F C_F} \;\Rightarrow\; C_F = \frac{1}{2\pi R_F f_{z1}} = \frac{1}{2\pi \cdot 75 \times 10^3 \cdot 7.45} = 285\,\text{nF} $$(24)
$$ f_{P3} = \frac{1}{2\pi R_3 (C_{\text{FB}} \parallel C_{\text{OPTO}})} \;\Rightarrow\; C_{\text{FB}} = \frac{1}{2\pi f_{P3} R_3} - C_{\text{OPTO}} = \frac{1}{2\pi \cdot 16.75 \times 10^3 \cdot 12 \times 10^3} - 200 \times 10^{-12} = 592\,\text{pF} $$设计好开环系统和补偿器后,利用公式(25)估算环路增益传递函数:
$$ G_{\text{TOTAL}}(s) = 38.2 \cdot \frac{ \left(1 - \frac{s}{2\pi \cdot 21.46 \times 10^3} \right) \left(1 + \frac{s}{2\pi \cdot 16.75 \times 10^3} \right) }{ \left(1 + \frac{s}{2\pi \cdot 74.5} \right) \left(1 + \frac{s}{2\pi \cdot 64.44 \times 10^3} \right) } \cdot \frac{ \left(1 + \frac{s}{2\pi \cdot 7.45} \right) }{ s \cdot \left( \frac{s}{2\pi \cdot 16.75 \times 10^3} + 1 \right) } $$公式(25)基于公式(13)和公式(18)。
计算相位和增益裕度对于确保电源的稳定性也非常重要。
相位裕度可以用公式(26)计算:
$$ \gamma = 180^\circ - \tan^{-1} \left( \frac{\omega_{C,\text{NEW}}}{\omega_{\text{RHP}}} \right) - \tan^{-1} \left( \frac{\omega_{z1}}{\omega_{C,\text{NEW}}} \right) + \tan^{-1} \left( \frac{\omega_{C,\text{NEW}}}{\omega_{\text{HF}}} \right) - \tan^{-1} \left( \frac{\omega_{C,\text{NEW}}}{\omega_{P1}} \right) - \tan^{-1} \left( \frac{\omega_{C,\text{NEW}}}{\omega_{P2}} \right) - \tan^{-1} \left( \frac{\omega_{C,\text{NEW}}}{\omega_{P3}} \right) $$输入相关值后,通过公式(27)计算出相位裕度:
$$ \gamma = 180^\circ - \tan^{-1} \left( \frac{6.5 \times 10^3}{21.46 \times 10^3} \right) - \tan^{-1} \left( \frac{7.45}{6.5 \times 10^3} \right) + \tan^{-1} \left( \frac{6.5 \times 10^3}{16.75 \times 10^3} \right) - \tan^{-1} \left( \frac{6.5 \times 10^3}{74.5} \right) - \tan^{-1} \left( \frac{6.5 \times 10^3}{64.44 \times 10^3} \right) - \tan^{-1} \left( \frac{6.5 \times 10^3}{16.75 \times 10^3} \right) = 68^\circ $$如果相位裕度超过50°,则该参数符合相关标准规范,具有重要设计意义。
与此同时,增益裕度可通过公式(28)近似计算得出:
$$ \gamma = 180^\circ - \tan^{-1} \left( \frac{\omega}{21.46 \times 10^3} \right) - \tan^{-1} \left( \frac{7.45}{\omega} \right) + \tan^{-1} \left( \frac{\omega}{16.75 \times 10^3} \right) - \tan^{-1} \left( \frac{\omega}{74.5} \right) - $$ $$ \tan^{-1} \left( \frac{\omega}{66.44 \times 10^3} \right) - \tan^{-1} \left( \frac{\omega}{16.75 \times 10^3} \right) = 0^\circ \;\Rightarrow\; \omega = 37.84\,\text{kHz} $$在指定频率下,通过公式(25)推导出公式(29):
$$ \left\| G_{\text{TOTAL}}(s) \right\| = 10^{\frac{38.2}{20}} \cdot \frac{ \sqrt{1 + \left( \frac{2\pi \cdot 37.84 \times 10^3}{2\pi \cdot 21.46 \times 10^3} \right)^2} \cdot \sqrt{1 + \left( \frac{2\pi \cdot 37.84 \times 10^3}{2\pi \cdot 16.75 \times 10^3} \right)^2} }{ \sqrt{1 + \left( \frac{2\pi \cdot 37.84 \times 10^3}{2\pi \cdot 74.5} \right)^2} \cdot \sqrt{1 + \left( \frac{2\pi \cdot 37.84 \times 10^3}{2\pi \cdot 66.44 \times 10^3} \right)^2} } \cdot \frac{ \sqrt{1 + \left( \frac{2\pi \cdot 7.5}{2\pi \cdot 37.84 \times 10^3} \right)^2} }{ \sqrt{1 + \left( \frac{2\pi \cdot 37.84 \times 10^3}{2\pi \cdot 16.75 \times 10^3} \right)^2} } $$ $$ \left\| G_{\text{TOTAL}}(s) \right\| = 0.282 \;\Rightarrow\; \left\| G_{\text{TOTAL}}(s) \right\|_{\text{dB}} = -11\,\text{dB} $$在此情况下,增益裕度低于-10dB ,这是需要重点考量的另一个重要参数,尤其涉及是否符合规范。若结果接近0dB ,则需通过多次迭代降低该值,否则系统将无法达到最佳性能。迭代必须首先从降低截止频率值着手。
至此,该完整传递函数通过以下方式为电源提供了最佳稳定性和性能:
- 最小化稳态误差
- 最大限度减少ESR寄生效应
- 将电源带宽提高至6.5kHz
最终设计
计算出反馈环路补偿器的所有无源元件值并确定变换器主要参数之后,即可采用HF500 -40 设计完整的反激式变换器。图 4 展示了利用所有计算参数得到的最终设计电路。
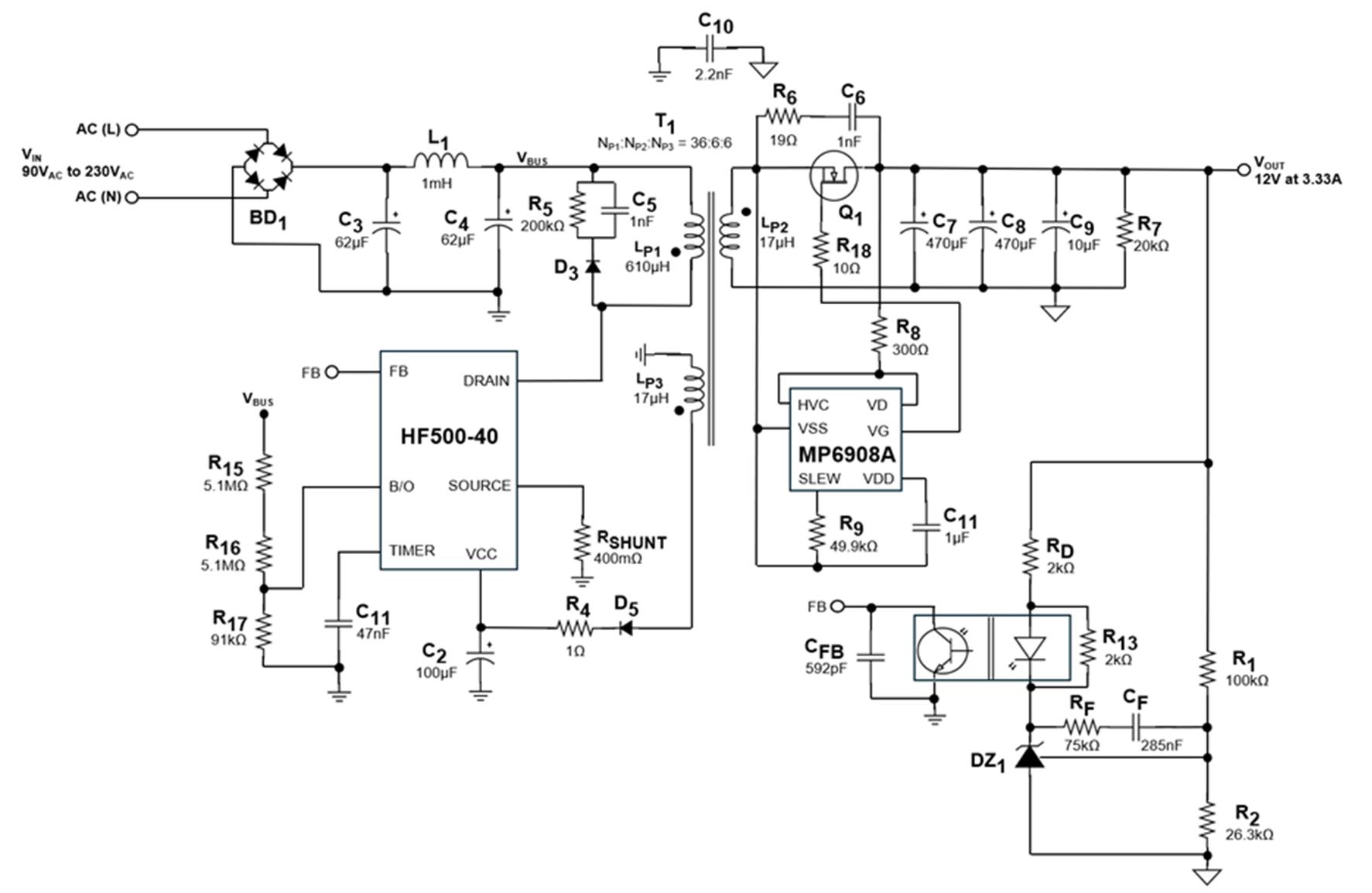
图4:最终设计电路原理图
图 5 为完整环路增益频率响应的波特图。
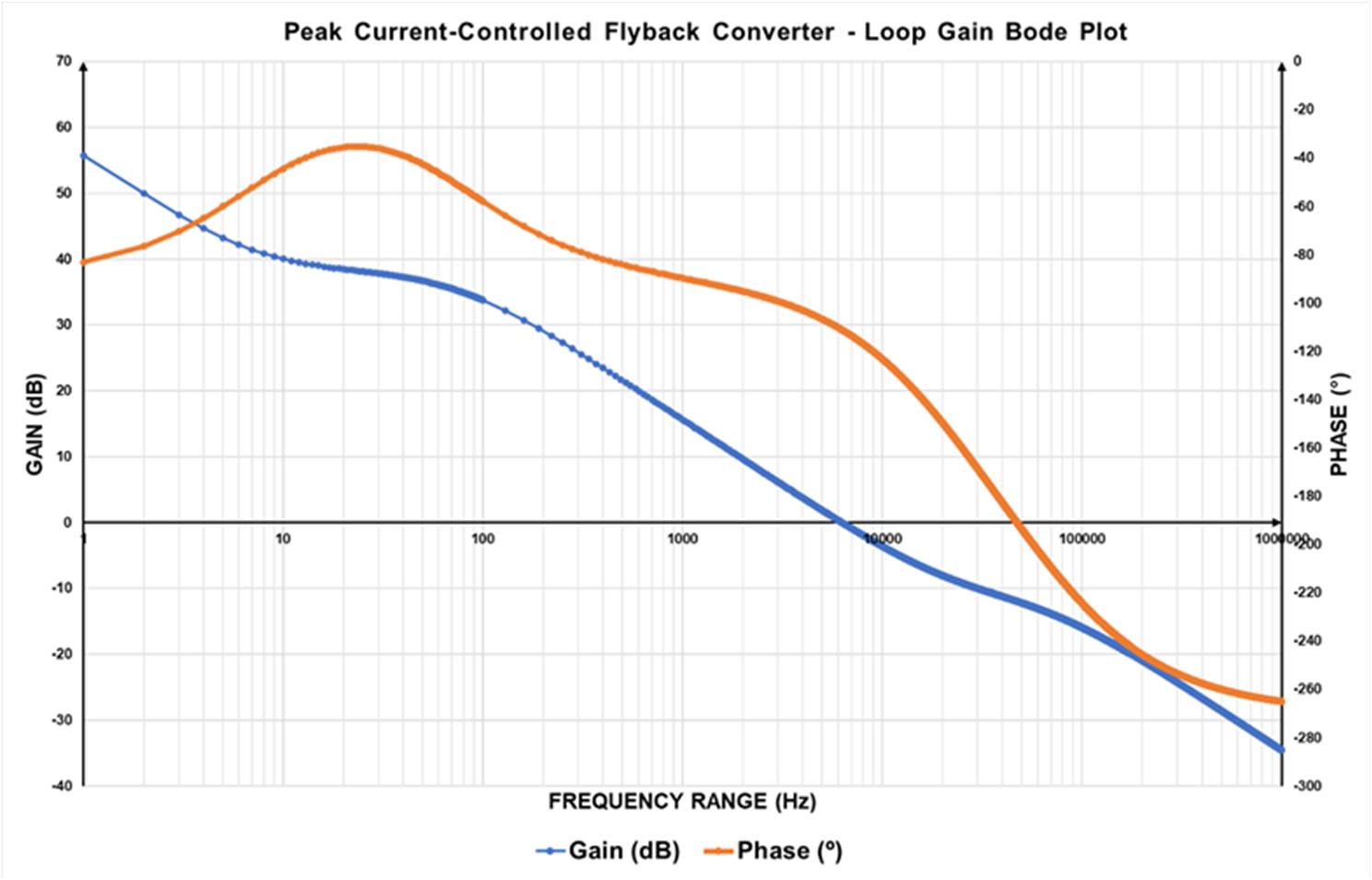
图5:完整环路增益频率响应波特图
结语
通过小信号分析获取反激式平均模型是一个复杂的过程,但能最精确地逼近变换器的传递函数。此外,交叉调节技术需要结合光耦反馈和可调电压基准实现副边调节,这进一步增加了计算复杂性。
然而,遵循本文所述的四个步骤,仍可获得良好近似值以提高电源性能,因其直接调节重载输出,使系统输出可以快速响应负载变化。由此可见,采用HF500-40设计光耦反馈补偿器 并不复杂。请继续探索MPS的副边调节 解决方案,以优化您的反激式拓扑设计。
_______________________
您感兴趣吗? 点击订阅,我们将每月为您发送最具价值的资讯!
技术论坛
 Latest activity 3 years ago
Latest activity 3 years ago
 9 回复
9 回复
 Latest activity 3 years ago
Latest activity 3 years ago
 3 回复
3 回复
 Latest activity 3 months ago
Latest activity 3 months ago
 9 回复
9 回复





直接登录
创建新帐号