Fundamentals of Developing Control Algorithms
To regulate the behavior of dynamic systems, digital control algorithms involve the development of mathematical models and computational procedures. By converting control objectives into executable instructions, these methods guarantee that the system performs within the intended performance specifications. The basic concepts of creating control algorithms, such as modeling, analysis, design, and implementation, are explored in this section.
Principles of Control Algorithm Development
Modeling the System: Develop a mathematical model which represents the dynamics of the system that has to be controlled.
Control Objectives: Specify the control objectives, including overshoot minimization, setpoint tracking, stability, and disturbance rejection.
Choice of Control Strategy: Based on the control objectives and the system model, choose a suitable control strategy.
Steps in Developing Control Algorithms
System Identification: Determine the system model's parameters analytically or through experiments.
Control Law Design: Establish the control law that defines how the output or state of the system is used to calculate the control inputs.
Stability Analysis: Examine the control system's stability to make sure it will hold up under all planned operating conditions.
Performance Analysis: Consider response time, overshoot, settling time, and steady-state error while assessing the control algorithm's performance.
Implementation Considerations: Consider the practical aspects of implementing the control algorithm, such as sampling rate, real-time constraints, and computational complexity.
Common Control Strategies
PID Control: A popular control strategy that combines derivative, integral, and proportional actions for achieving the desired system behavior.
State-Space Control: Utilize a state-space representation of the system, in which a collection of differential equations of the first order describes the state of the system.
Adaptive Control: Adjust the control parameters in real time in response to changes in operating conditions or system dynamics.
Optimal Control: Develop a control law that reduces or increases a specific performance metric, such as energy usage or tracking error.
Example: Developing a PID Control Algorithm for Temperature Regulation
Modeling the System:
Step: Develop a thermal model of the system, incorporating thermal capacitance and heat transfer dynamics.
Equation:
$$ \frac{dT(t)}{dt} = \frac{Q(t) - k(T(t) - T_{\text{ambient}})}{C} $$where C is the thermal capacitance, k is the heat transfer coefficient, Q(t) is the heat input, and T(t) is the temperature.
Control Objectives:
Maintain temperature within ±0.5°C of setpoint, even with ambient temperature fluctuations.
Designing the PID Controller:
Proportional Term:
$$ P = K_p e(t) $$Integral Term:
$$ I = K_i \int_{0}^{t} e(\tau) \, d\tau $$Derivative Term:
$$ D = K_d \frac{d e(t)}{dt} $$Where
$$ e(t) = T_{\text{setpoint}} - T(t) $$is the error signal.
Control Law:
$$ Q(t) = P + I + D $$Tuning the PID Parameters:
Ziegler-Nichols Method: Determine the initial values of Kp, Ki, and Kd using the Ziegler-Nichols tuning rules.
Stability and Performance Analysis:
Simulation: Simulate the closed-loop response to disturbances and a step change in the setpoint.
Evaluation: Measure the rise time, overshoot, settling time, and steady-state error to confirm they satisfy the required specifications.
Implementation:
Microcontroller: Implement the PID algorithm on a microcontroller, making sure it runs within the sampling period and handles real-time limitations.
Techniques for Implementing Algorithms in Microcontrollers and DSPs
Implementing digital control algorithms in microcontrollers (MCUs) and digital signal processors (DSPs) entails converting theoretical control strategies into executable code that runs efficiently on hardware platforms. This procedure necessitates a detailed knowledge of both control algorithms and hardware capabilities. This section explores the major techniques and considerations for creating control algorithms in MCUs and DSPs.
Overview of Microcontrollers and DSPs
Microcontrollers (MCUs): general-purpose Processors developed for applications with embedded control. They integrate a CPU with communication interfaces, memory, timers, and I/O peripherals.
Digital Signal Processors (DSPs): specialized processors designed to perform numerical computations fast, especially for tasks involving real-time signal processing. They frequently have hardware multipliers and tailored instruction sets.
Techniques for Implementing Control Algorithms
Algorithm Optimization for Real-Time Execution: To meet real-time requirements, ensure that the control algorithm is executed within the time limits.
Fixed-Point Arithmetic: To reduce computational overhead and enhance execution speed on MCUs with limited processing power, use fixed-point arithmetic rather than floating-point.
Efficient Memory Management: Optimize memory resources to efficiently store lookup tables, algorithm variables, and coefficients.
Interrupt-Driven Execution: To trigger the execution of control algorithms in response to particular events or timing requirements, use hardware interrupts.
Modular and Reusable Code: Write code that is modular so that it can be easily modified and reused for various control applications.
Specific Techniques for Microcontrollers
Hardware Abstraction Layer (HAL): To make interfacing with MCU hardware and peripherals simpler, use HAL libraries.
Direct Memory Access (DMA): Data handling and processing can be done more efficiently by using DMA to relieve the CPU of data transfer tasks.
Real-Time Operating Systems (RTOS): For complicated control applications, use RTOS to regulate resource allocation, task scheduling, and timing.
Specific Techniques for DSPs
Optimized Instruction Sets: Make use of DSPs' unique instruction sets and hardware capabilities to accelerate the execution of control algorithms.
Parallel Processing: Use DSPs' parallel processing capability to carry out multiple operations at once.
Adaptive Filtering and Control: Use control algorithms and adaptive filtering to dynamically modify parameters in response to real-time data.
Software Tools and Environments for Algorithm Development
It takes a combination of theoretical design, simulation, testing, and implementation to develop digital control algorithms. These tasks are significantly helped by software tools and environments, which give engineers the platforms they need to effectively model, simulate, test, and implement control algorithms. The features, advantages, and uses of the many software tools and environments utilized in the creation of digital control algorithms are explored in this section.
Overview of Software Tools and Environments
MATLAB and Simulink: Programming, visualization, and numerical computation are all done with MATLAB, a high-level language and interactive environment. An extension of MATLAB, Simulink offers a graphical environment for dynamic system modeling, simulation, and analysis.
LabVIEW: National Instruments offers a system-design platform and development environment for visual programming called Laboratory Virtual Instrument Engineering Workbench (LabVIEW).
Embedded C/C++: Designed for programming embedded systems, embedded C/C++ is an extension of the C and C++ programming languages.
Code Composer Studio (CCS): Texas Instruments' integrated development environment (IDE), designed specifically for its DSPs and microcontrollers, offers tools for embedded software deployment, optimization, and debugging.
Keil µVision: An integrated development environment (IDE) that provides extensive simulation and debugging capabilities for ARM-based microcontrollers.
Features and Benefits of Software Tools
Model-Based Design: Designed to create models that accurately depict physical systems, allowing for analysis and simulation prior to hardware implementation.
Real-Time Simulation and Testing: Enables iterative development and validation by facilitating real-time simulation and testing of control algorithms.
Automatic Code Generation: Automatically creates C/C++ code from high-level models or algorithms, cutting down on errors and the time and effort required for manual coding.
Integrated Debugging and Optimization: Improves performance and reliability by offering integrated debugging and optimization tools to find and fix issues in the control algorithms.
Applications and Use Cases
Automotive Control Systems:
Tools: Code Composer Studio, Embedded C/C++, and MATLAB/Simulink.
Application: developing and assessing control algorithms for advanced driver-assistance systems (ADAS), engine management, and transmission control.
Industrial Automation:
Tools: MATLAB/Simulink, KeilVision, and LabVIEW.
Application: Implementing and optimizing control systems for robotics, automated test equipment, process control.
Consumer Electronics:
Tools: MATLAB/Simulink, Keil Vision, and embedded C/C++.
Application: Developing control algorithms for wearable technologies, home automation systems, and smart devices.
Renewable Energy Systems:
Tools: LabVIEW, Code Composer Studio, and MATLAB/Simulink.
Application: Developing control strategies for battery management systems, wind turbine controllers, and solar inverters.
Practical Examples and Case Studies of Algorithm Implementation
Case studies and real-world examples are crucial for comprehending how digital control algorithms are used in the real world. They shed light on the challenges, methodologies, and solutions in implementing these algorithms into various systems. The design, implementation, and optimization of digital control algorithms across various sectors and applications are demonstrated by the real-world examples and case studies are explored in this section.
Practical Example 1: PID Control of a DC Motor
System Description:
Objective: Implement a PID control algorithm to control a DC motor's speed.
Components: Motor driver, microcontroller (such as an Arduino), DC motor, and rotary encoder (for feedback).
Algorithm Development:
Modeling: Design a mathematical model of the motor dynamics that includes back EMF, inductance, and resistance.
Control Objectives: Despite changes in the load, keep the motor speed at a setpoint.
PID Tuning: The proportional (Kp), integral (Ki), and derivative (Kd) gains can be determined using Ziegler-Nichols or trial-and-error methods.
Implementation:
Microcontroller Programming: Write the PID control algorithm in C/C++ and upload it to Arduino.
Feedback Loop: To measure the motor speed and give the PID controller feedback, use the rotary encoder.
Testing and Optimization:
Initial Testing: Run the motor and monitor the response to step changes in the setpoint.
Optimization: To reduce overshoot, settling time, and steady-state error, adjust the PID gains.
Validation: To ensure robustness, check the performance under various load conditions.
Practical Example 2: Temperature Control in an HVAC System
System Description:
Objective: Develop a digital control system that uses an HVAC system to maintain a specified room temperature.
Components: Actuators, heating and cooling components, temperature sensors, and microcontrollers (e.g. STM32).
Algorithm Development:
Modeling: Develop a thermal model of the room while taking external disturbances, heat capacity, and heat transfer into account.
Control Objectives: Maintain the room temperature within a small range of the setpoint.
Control Strategy: For known disturbances (like sunlight), use a PID control algorithm with additional feedforward compensation.
Implementation:
Microcontroller Programming: Deploy the control algorithm to the STM32 microcontroller after writing it in C.
Sensor Integration: Connect temperature sensors to the microcontroller to get feedback in real time.
Actuator Control: Using the PID controller's output, regulate the heating and cooling components of the HVAC system.
Testing and Optimization:
Simulation: To validate the control algorithm and simulate the room's thermal response, use MATLAB/Simulink.
Real-World Testing: Perform testing in an actual room environment, modifying the control parameters in response to performance observations.
Optimization: Optimize the algorithm to increase comfort, reduce energy use, and improve response time.
Practical Example 3: Adaptive Cruise Control in Automobiles
System Description:
Objective: Create an adaptive cruise control (ACC) system that, when cruising at a predetermined speed, maintains a safe distance from the vehicle in front.
Components: Microcontrollers or DSPs, lidar or radar sensors, and actuators for throttle and braking.
Algorithm Development:
Modeling: Make a dynamic model of the longitudinal motion of the vehicle while taking external forces, acceleration, and deceleration into account.
Control Objectives: Depending on traffic conditions, modify the following distance while maintaining the desired speed.
Adaptive Control: Implement an adaptive control algorithm that modifies control parameters in real time depending on sensor data.
Implementation:
Sensor Integration: Interface lidar or radar sensors to the microcontroller to measure distance and relative speed and to detect vehicles.
Control Algorithm: Develop the integrated C/C++ control algorithm and implement it on the DSP or microcontroller.
Actuator Control: Use the control algorithm to regulate the braking actuators and the throttle.
Testing and Validation:
Simulation: Validate the control algorithm by simulating the ACC system using a high-fidelity vehicle dynamics model.
Real-World Testing: Test the ACC system on a test track and monitor how well it performs in different traffic conditions.
Optimization: To guarantee seamless safe operation, adjust the algorithm and control parameters in response to test results.
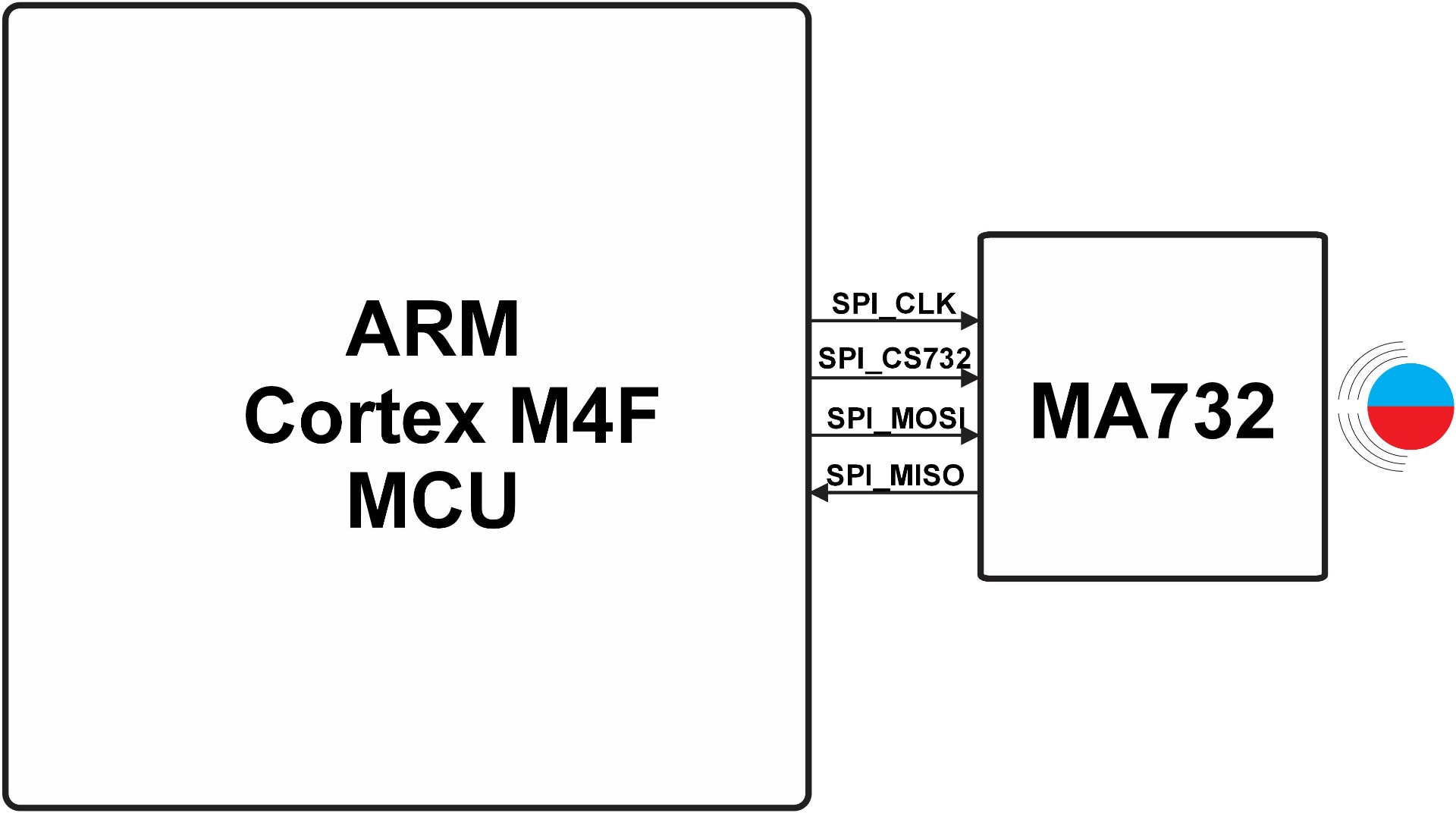
Practical Example 4: Power Inverter Control for Renewable Energy Systems
System Description:
Objective: Implement a digital control algorithm for a power inverter, which converts DC electricity from solar panels to grid-ready AC power.
Components: Grid interface, microcontroller or DSP, power inverter, and solar panels.
Algorithm Development:
Modeling: Design a model of the power conversion procedure that incorporates the grid interface and the electrical properties of the inverter.
Control Objectives: Optimize the efficiency of power transfer, guarantee steady operation, and abide by grid regulations.
Control Strategy: Use a Maximum Power Point Tracking (MPPT) algorithm alongside current control and grid synchronization.
Implementation:
MPPT Algorithm: Design the MPPT algorithm to continuously modify the solar panels' operating point for optimal efficiency.
Grid Synchronization: Use current control and phase-locking algorithms to make sure the inverter's output is in sync with the grid.
Firmware Development: Write the C/C++ control algorithms and then implement them on the DSP or microcontroller.
Testing and Optimization:
Laboratory Testing: Use simulated grid conditions and variable loads to test the inverter control system in a controlled laboratory environment.
Field Testing: Install the inverter in a real solar power system and track its operation over time.
Optimization: Adjust the control algorithms to increase grid standard compliance, stability, and efficiency.
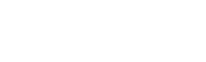






直接登录
创建新帐号